기본 정렬 알고리즘의 종류와 정리
최종수정일자 : 2020-01-03
이 글은 이미 공부 했었으나, 정렬을 쉽게 정리하지 못하는 사람을 위해 정리하였다.
정렬의 종류도 많으며, 설명하기가 쉽지 않다.
동작은 다양하며, 머리속에 어렴풋이 남는 경우가 많다.
필자도 그렇다.
머리가 나빠서 그런지 매번 까먹고, 설명할 때 순서가 없고 중구난방의 문제를 겪었다.
정리의 목적과 목표
- 누군가에게 설명하기 위한 정렬 공부를 목적으로 한다.
- 정의 만으로 알고리즘을 유추할 수 있도록 한다.
- 정렬을 머리에 쉽게 넣고 기억에 잘 남길 수 있도록 하는 나만의 정리 기법으로 답을 낸다.
- 많은 내용을 머리에 넣지 않는다. (앞으로 알아야 할 것이 많기 때문에 모두 다 못 넣는다.
왜 정렬 알고리즘을 알아야 하는가?(why)
학부 시절 때 알고리즘 과목을 들으면 정렬을 배운다.
왜 우리는 정렬을 알아야 하는가? 스스로가 정한 답이다.
- 정렬의 큰 개념 확립
- 정렬을 배움으로써 알고리즘의 본질을 '더' 깨우침
- '더' 어려운 문제를 풀기위한 기초
정렬의 기초 연산
일반적으로 두 가지 연산을 해야 한다.
- 판별 및 비교
- 교환
무엇을 할 것인가?(What)
- 선택정렬
- 삽입정렬
- 간접정렬
- 쉘정렬
- 버블정렬
- 분포수세기
- 퀵정렬
- 병합정렬
- 기수교환정렬
- 직접기수정렬
- 기수정렬
- 힙정렬
어떻게 머리에 잘 넣을 수 있는가?(How)
- 정렬을 짧은 한 문장으로 정의한다.
- 정의를 통해 머리속에 알고리즘을 유추한다.
- 키워드 만 추출하여 힌트를 얻는다.
- 힌트를 통해 동작을 출력한다.
문서의 규칙
- 생략 가능한 글자는 괄호를 이용한다.
- 정렬의 정의는 나름대로 20자 이내(띄어쓰기 비포함)로 정의한다.
- 정의에는 핵심 동작이 들어있어야 한다.
- 많은 것을 머리속에 넣지 않는다.
첫 번째 예시를 통해, 어떻게 정렬을 한 문장으로 정의할 수 있는지 살펴보자.
선택정렬
- 정의 : (순차적으로) 가장 작은 수를 선택하고 (반복) 교환하는 정렬
- 시간복잡도 : O(N^2)
- 안정성 : 없음
- 자료의 집합에서 (순차적으로) 가장 작은 수를 선택한다.
- 교환한다.
- (반복)한다.
그림으로 표기하면 다음과 같다.

정의와 동작(그림)을 머리속에 매칭해보자.
자료의 집합에서 전체탐색을 통한 가장 작은 수를 먼저 찾아야 한다.
가장 작은 수와 현재 인덱스(i)와 교환한다.
다음 인덱스(i+1)을 시작으로 다시 가장 작은 수를 먼저 찾는다.
핵심 동작은 가장 작은 수를 선택하고 교환하는 행위다.
알고리즘
public class SelectSort {
/**
* 알고리즘
* 1. i = 0
* 2. i부터 N-1까지 가장 크거나 작은값을 찾는다.
* 3. i와 가장 크거나 작은값을 교환한다. 동일한 값일 경우 교환하지 않는다.
* 4. ++i
* 5. 2부터 다시 반복한다.
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1};
public void sort() {
for (int i = 0; i < value.length; i++) {
int minIndex = i;
int min = value[minIndex];
for (int j = i; j < value.length; j++) {
// TODO : 중요! < 와 <= 는 엄연하게 Stability 관점에서 교환하냐 안하냐가 달라질 수 있다.
if (value[j] < min) {
min = value[j];
minIndex = j;
}
}
swap(value, i, minIndex);
}
printValue();
}
private void swap(int array[], int index1, int index2) {
int tempValue = array[index1];
array[index1] = array[index2];
array[index2] = tempValue;
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i=0;i<value.length;i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}삽입정렬
- 정의 : (자기 보다) 작은 수가 나올 때 까지 우 로 밀어 삽입하는 정렬
- 시간복잡도 : O(N^2)
- 안정성 : 일반적으로 있음
- (자기보다) 왼쪽에 작은 수가 나올 때 까지 우 로 민다.
- 왼쪽에 (자기 보다) 작은 수가 나오면 삽입한다.
- (반복)한다.
그림으로 표기하면 다음과 같다.

정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
자기(i)보다 왼쪽의 작은 수가 나올 때 까지 데이터를 우 로 밀어 빈 곳에 자기(i)를 삽입한다.
다음 인덱스(i+1)를 시작으로 다시 왼쪽의 작은 수가 나올 때 까지 데이터를 우 로 밀어 빈 곳에 자기(i+1)를 삽입한다.
핵심 동작은 작은 수가 나올 때 까지 우로 밀어 삽입 하는 것이다.
알고리즘
public class InsertionSort {
/**
* 알고리즘
* 1. i = 1
* 2. j = i;
* 3. t = arr[i]
* 3. array[j-1] > array[i] && j > 0 인동안
* 3-1. array[j] = array[j-1];
* 3-2. j--;
* 4. arr[j] = t;
* 5. i++; 반복
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1};
public void sort() {
for (int i = 1; i < value.length; i++) {
int j = i;
int t = value[i];
while (j > 0 && value[j - 1] > t) {
value[j] = value[j - 1];
j--;
}
value[j] = t;
}
printValue();
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i=0;i<value.length;i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}
간접정렬
- 정의 : 값의 배열이 아닌 인덱스 배열을 조작하는 정렬
- 시간복잡도 : 삽입 정렬 시 O(N^2)
- 안정성 : 삽입 정렬 시 일반적으로 있음
- 값의 배열을 기준으로 비교하여 (자기 보다) 왼쪽에 작은 수가 나올 때 까지 인덱스 값을 우 로 민다.
- 값의 배열을 기준으로 비교하여 왼쪽에 (자기 보다) 작은 수가 나오면 인덱스 값을 삽입한다.
- (반복)한다.
그림으로 표기하면 다음과 같다.

정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 값의 배열이 아닌 별도의 인덱스 배열을 조작 하는 것이다.
알고리즘
public class IndirectInsertionSort {
int value[] = {5, 3, 8, 2, 10, 9, 4, 1};
int index[] = {0, 1, 2, 3, 4, 5, 6, 7};
public void sort() {
for (int i = 1; i < value.length; i++) {
int j = i;
int t = index[i];
while (j > 0 && value[index[j - 1]] > value[t]) {
index[j] = index[j - 1];
j--;
}
index[j] = t;
}
printValue();
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i=0;i<index.length;i++) {
builder.append(value[index[i]]).append(" ");
}
System.out.println(builder.toString());
}
}
거품정렬
- 정의 : 좌측 값이 자기 보다 크면 교환하는 정렬 OR 우측 값이 자기 보다 작으면 교환하는 정렬
- 시간복잡도 : O(N^2)
- 안정성 : 일반적으로 있음
- 좌측 값이 자기 보다 크면 교환한다.
- (반복)한다.
그림으로 표기하면 다음과 같다. (좌측 값이 크면 교환하는 정렬)
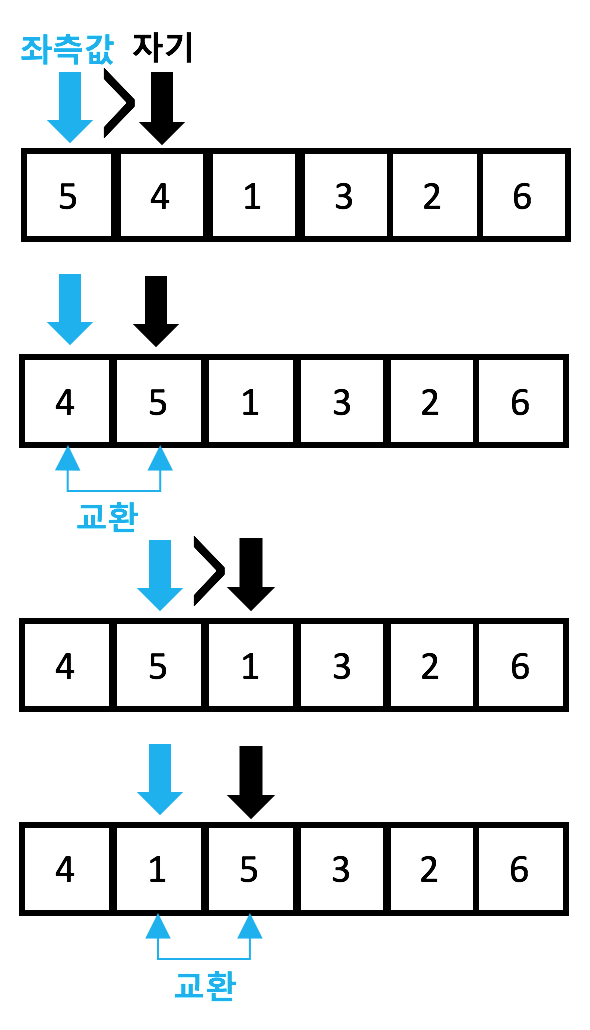
정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 좌측 값이 자기 보다 크면 교환 하는 것이다.
알고리즘
public class BubbleSort {
/**
* 알고리즘
* 1. i = 0;
* 2. i가 n-1이면 끝낸다.
* 3. j = 1;
* 4. j가 n-i가 되면 7로 간다.
* 5. a[j-1] > a[j] 이면 두 값을 교환한다,
* 6. j를 하나 증가시키고 4로 돌아간다.
* 7. i를 하나 증가시키고 2로 돌아간다.
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1};
public void sort() {
for (int i = 0; i < value.length - 1; i++) {
for (int j = 1; j < value.length - i; j++) {
if (value[j - 1] > value[j]) {
swap(value, j - 1, j);
}
}
}
printValue();
}
private void swap(int array[], int index1, int index2) {
int tempValue = array[index1];
array[index1] = array[index2];
array[index2] = tempValue;
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i=0;i<value.length;i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}
쉘 정렬
- 정의 : (자기 보다) 작은 수가 나올 때 까지 간격 만큼 우로 밀어 삽입하는 (정렬)
- 시간복잡도: 평균 O(N^1.5) 최악 O(N^2)
- 안정성 : 없음
- 간격은 Hn = 3 *H(n-1) + 1, n = 데이터 수
- (자기보다) 왼쪽에 작은 수가 나올 때 까지 간격 만큼 우 로 민다.
- 왼쪽 간격에 (자기 보다) 작은 수가 나오면 삽입한다.
- (반복)한다.
- 간격을 줄인다.
- 1번 부터 (반복)한다.
그림으로 표기하면 다음과 같다. (삽입정렬과 같으나 간격만큼 우로 민다.)

정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 삽입정렬과 같되 간격 만큼 비교하고 우로 미는 정렬이다.
점점 간격을 줄여 나간다.
알고리즘
public class ShellSort {
/**
* 알고리즘
* 1. Gap의 초기값을 구한다.
* 2. Gap가 1보다 작으면 끝낸다.
* 3. k = 0;
* 4. k가 Gap보다 크거나 같으면 7로 간다.
* 5. (Gap간격 + k) 요소들에 대해서 삽입정렬을 한다.
* 6. k를 하나 증가시키고 4로 간다.
* 7. Gap의 다음 값을 구하고 2로 간다.
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1};
public void sort() {
// TODO : 여기서는 Gap을 배열 사이즈의 / 2로 기준 잡음.
for (int gap = value.length / 2; gap > 0; gap /= 2) {
for (int k = 0; k < gap; k++) {
// TODO : 간격을 중심으로 삽입정렬을 한다.
for (int i = k + gap; i < value.length; i += gap) {
int j = i;
int t = value[i];
while (j >= gap && value[j - gap] > t) {
value[j] = value[j - gap];
j -= gap; // 간격만큼 감소한 인덱스
}
value[j] = t;
}
}
}
printValue();
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < value.length; i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}
분포수세기 정렬
- 정의 : 빈도를 누적분포로 저장하고 인덱스로 읽어 삽입(하는 정렬)
- 시간복잡도 : O(N)
- 안정성 : 일반적으로 있음
- 값의 빈도를 누적분포로 저장한다.
- 배열을 뒤에서 부터 읽는다.
- 새로운 배열에 빈도를 인덱스로 읽어 삽입한다.
- 빈도 수를 감소시킨다.
- 2번 부터 (반복)한다.
그림으로 표기하면 다음과 같다.

정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 빈도를 누적분포로 저장하고 인덱스(빈도수 -1) 로 읽어 삽입 하는 정렬이다.
안정성을 위해 뒤에서 부터 읽는다.
알고리즘
public class DistributionCounting {
/**
* 알고리즘
* 1. count[] 배열을 0으로 초기화
* 2. array[] 배열의 키의 빈도를 계산하여 그 빈도를 count[]에 저장
* 3. count[] 배열을 누적분포로 변환
* 4. array[] 배열을 뒤에서부터 읽어서(--) b[--count[array[i]]에 저장
* 5. b[] 배열을 a[] 배열로 복사한다.
* <p>
* 예시
* 1 3 2 2 3 1 3 2 4
* count[1] = 2 (1의 갯수)
* count[2] = 3 (2의 갯수)
* count[3] = 3 (3의 갯수)
* count[4] = 1 (4의 갯수)
* <p>
* 누적분포화
* <p>
* count[1] = 2
* count[2] = count[1] + count[2] (5)
* count[3] = count[2] + count[3] (8)
* count[4] = count[3] + count[4] (9)
*/
int value[] = {1, 3, 2, 2, 3, 1, 3, 2, 4};
int temp[] = {0, 0, 0, 0, 0, 0, 0, 0, 0};
int count[] = {0, 0, 0, 0, 0};
public void sort() {
for (int i = 0; i < value.length; i++) {
++count[value[i]];
}
for (int i = 2; i <= 4; i++) {
count[i] = count[i - 1] + count[i];
}
for (int i = value.length -1; i >= 0; i--) {
temp[--count[value[i]]] = value[i];
}
printValue();
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < temp.length; i++) {
builder.append(temp[i]).append(" ");
}
System.out.println(builder.toString());
}
}
퀵 정렬
- 정의 : 좌측, 우측 값을 축 값과 비교하고 (서로) 교환 후 (재귀적으로) 분할 하는 정렬
- 시간복잡도 : O(Log2N), O(NlogN)
- 안정성 : 없음
- 좌측 값이 '축' 값 보다 크거나 같은 것을 찾을 때 까지 비교한다.
- 우측 값이 '축' 값 보다 작거나 같은 것을 찾을 때 까지 비교한다.
- 좌측 값과 우측 값을 교환한다.
- 좌측 인덱스가 우측 인덱스보다 크면 배열을 분할한다.
- 재귀적으로 (반복)한다.
그림으로 표기하면 다음과 같다.
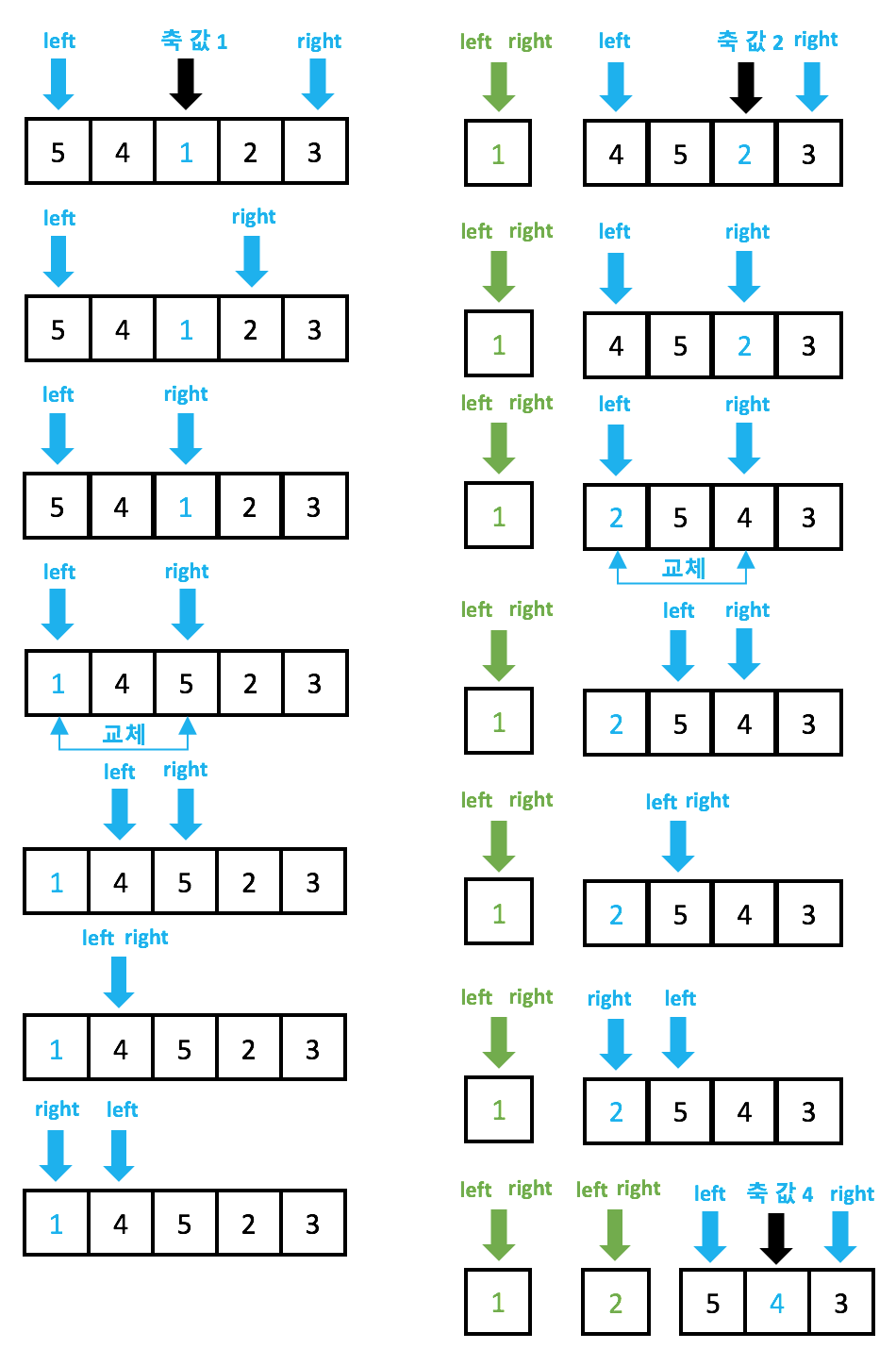
정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 축 값과 좌측 값 또는 축 값과 우측 값을 비교 후 좌측 값과 우측 값을 교환한다.
좌측 인덱스가 우측 인덱스보다 크면 배열을 분할한다.
데이터 배열이 역순일 경우 최악의 경우다.
알고리즘
public class QuickSort {
/**
* 알고리즘
* 1. 만약 right > left 이면
* 1-1 N 크기의 a 배열을 분할하여 축값의 위치를 mid로 넘긴다.
* 1-2 퀵 정렬 알고리즘(array, left, mid)
* 1-3 퀵 정렬 알고리즘(array, mid, right),
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1, 7, 6, 6, 12, 8, 11, 9};
public void sort() {
printValue();
quicksort(value, 0, value.length - 1);
printValue();
}
private void quicksort(int array[], int left, int right) {
if (left >= right) {
return;
}
int tempLeft = left - 1;
int tempRight = right + 1;
int pivotValue = array[(left + right)/2]; // 중위값으로 선택
while (true) {
while (array[++tempLeft] < pivotValue);
while (pivotValue < array[--tempRight]);
if (tempLeft > tempRight) break;
swap(array, tempLeft, tempRight);
}
quicksort(array, left, tempRight);
quicksort(array, tempLeft, right);
}
private void swap(int array[], int index1, int index2) {
int tempValue = array[index1];
array[index1] = array[index2];
array[index2] = tempValue;
}
private void printValue() {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < value.length; i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}
병합 정렬
- 정의 : (최소 단위 까지) 배열을 (재귀적으로) 분할 후, 병합 시 (부분 배열의) 앞에서 부터 비교 삽입 하는 정렬
- 시간복잡도 : O(NLogN)
- 안정성 : 안정성 있다.
- 배열을 (최소 단위 까지) 분할 한다.
- 병합 시, 부분 배열의 각 앞에서 부터 순차 비교 후 임시 배열에 삽입한다.
- 임시 배열을 원본 배열에 복사한다.
- (반복)하여 병합한다.
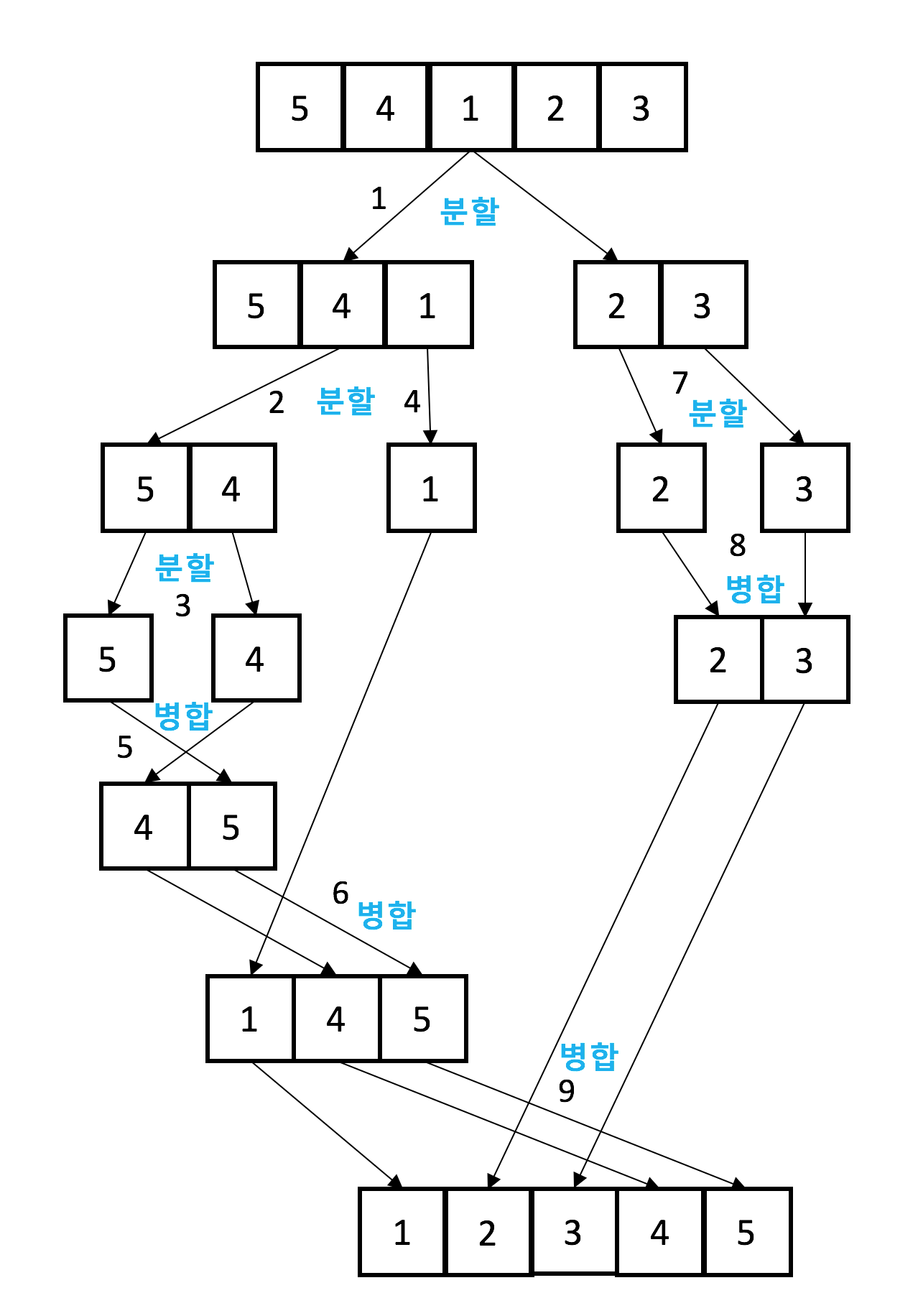
정의와 동작(그림)을 머리속에 매칭해보자. 매칭해보도록 노력하자.
핵심 동작은 최소 단위 까지 분할 하고 병합 시, 두 배열을 순차적으로 앞에서 부터 작은 값을 임시 배열에 삽입 하는 방식을 택한다.
알고리즘
public class MergeSort {
/**
* 알고리즘
* 1. l < r 인경우
* 1) mid = (l + r) / 2
* 2) mergeSort(l, mid)
* 3) mergeSort(mid + 1, r)
* 4) merge(l, mid, r)
*/
int value[] = {5, 3, 8, 2, 10, 9, 4, 1, 7, 6, 6, 12, 8, 11, 9};
public void sort() {
int newValue[] = mergeSort(value, 1);
// mergeSort2(value, 0, value.length - 1);
printValue(newValue);
}
public int[] mergeSort(int inputArray[], int n) {
if (n >= inputArray.length) {
return inputArray;
}
int firstIndex = 0;
int secondIndex = firstIndex + n;
int temp[] = new int[inputArray.length];
int tempIndex = 0;
while (firstIndex < inputArray.length) {
int i = firstIndex;
int j = secondIndex;
while (true) {
boolean isExistFirstIndex = i < inputArray.length && i < (firstIndex + n);
boolean isExistSecondIndex = j < inputArray.length && j < (secondIndex + n);
if (isExistFirstIndex && isExistSecondIndex) {
if (inputArray[i] <= inputArray[j]) {
temp[tempIndex++] = inputArray[i++];
} else {
temp[tempIndex++] = inputArray[j++];
}
} else if (isExistFirstIndex) {
temp[tempIndex++] = inputArray[i++];
} else if (isExistSecondIndex) {
temp[tempIndex++] = inputArray[j++];
} else {
break;
}
}
firstIndex = firstIndex + (n * 2);
secondIndex = firstIndex + n;
}
return mergeSort(temp, n * 2);
}
public void mergeSort2(int inputArray[], int l, int r) {
if (l < r) {
int mid = (l + r) / 2;
mergeSort2(inputArray, l, mid);
mergeSort2(inputArray, mid + 1, r);
merge(inputArray, l, mid, r);
}
}
public void merge(int inputArray[], int l, int mid, int r) {
int tempArray[] = new int[r - l + 1];
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (inputArray[i] <= inputArray[j]) {
tempArray[k++] = inputArray[i++];
} else {
tempArray[k++] = inputArray[j++];
}
}
for (; i <= mid; ) {
tempArray[k++] = inputArray[i++];
}
for (; j <= r; ) {
tempArray[k++] = inputArray[j++];
}
for (int n = 0; n < tempArray.length; n++) {
inputArray[l + n] = tempArray[n];
}
}
private void printValue(int value[]) {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < value.length; i++) {
builder.append(value[i]).append(" ");
}
System.out.println(builder.toString());
}
}
힙 정렬
- 정의 : 우선순위 큐를 이용, 다운 힙, 업 힙 연산으로 정렬
- 시간복잡도 : O(NLogN)
- 안정성 : 동일한 값에 대한 기준이 별도로 있어야 한다. 또는 동일한 값의 존재를 부정한다.
기수 교환 정렬
- 정의 : 값을 비트로, 0과 1로 비교 교환 하는 유사 퀵 정렬
- 시간복잡도 : O(NLogN)
- 안정성 : 동일한 값에 대한 기준이 별도로 있어야 한다. 또는 동일한 값의 존재를 부정한다.
- 제한 : 값 들이 동일한 비트 수를 가져야 한다.
계속 정리중...